Modellbau: Grundlagen
Antriebe und Getriebe
Das Thema dieser Seite sind Motore und Getriebe, besonders im Hinblick auf Modelleisenbahn–Triebfahrzeuge (Lokomotiven und Triebwagen).
In den jeweiligen Abschnitten finden Sie auch die nötigen Formeln zur Getriebeberechnung
und Getriebeauslegung (ohne Berücksichtigung der Belastbarkeit).
Abschnitte dieser Seite:
- Antriebsquellen
- Bestimmung der Motordrehzahl
- Stirnzahnrad–Getriebe
- Schnecken–Getriebe
- Getriebe–Auslegung für Fahrzeuge
- Schwungmassen
Antriebsquellen
Bei der Modellbahn werden hauptsächlich thermodynamische (Heizdraht, Bimetall mit Wicklung),
elektromagnetische (Spulen, Eisenkern) und motorische Antriebe verwendet. Näheres zu Spulenantrieben
findet sich im Bereich Elektrik.
Bei Elektromotoren sind üblich: konventionelle, 3–, 5– und 7–polige Typen sowie Glockenankermotore („Faulhaber–Motoren”). Je höher die Polzahl eines
Motors ist, desto besser ist sein Rund– und Anlaufverhalten, da der Winkel zwischen den aufgebauten magnetischen Feldern kleiner wird.
Kein konventionell gebauter Motor erreicht einen so guten Wirkungsgrad, eine so gute Linearität
im Drehmomentverlauf und einen so ruhigen Lauf wie ein bürstenloser Glockenankermotor.
Außerdem haben solche Motore fast stets eine Drehzahlkonstante. Diese Zahl gibt die Umdrehungen des Motors je Minute und Volt Spannung an.
Wichtig sind auch Betriebsspannung und Stromaufnahme, beides wieder Elektrothemen,
sowie der Leerlauf– und Lastdrehzahl. Letztere ist maßgeblich für eine eventuell
notwendige Getriebe–Untersetzung. Das Drehmoment eines Antriebs steigert sich durch eine
Untersetzung, die Drehzahl am Ende des Getriebes verringert sich.
Bestimmung der Motordrehzahl
Wenn Ihnen die Leerlauf– oder Lastdrehzahl eines Motors unbekannt ist, können Sie
eine Stroboskop–Scheibe (siehe Abbildung) verwenden, um die Drehzahl in etwa zu bestimmen. Eine solche Scheibe zum Ausdrucken finden Sie bei den
Downloads (für die Sie sich zunächst registrieren müssen).
Schneiden Sie die Scheibe sauber aus und bohren Sie in der Mitte ein Loch, das etwas kleiner ist
als die Motorwelle. Schieben Sie nun die Scheibe möglichst gerade auf. Dann
schließen Sie den Motor an eine Spannungsquelle mit der Nennspannung an.
Beleuchten Sie nun die Scheibe mit einer Leuchtquelle, die mit Wechselstrom betrieben wird, am besten einer Neonröhre
oder Leuchtstoff–Lampe. Wenn Sie die Spannung geringfügig nach oben oder unten verändern, wird es irgendwann
so aussehen, als ob einer der Ringe der Scheibe fast still steht. Wenn ein benachbarter Ring sich ebenfalls
nur langsam dreht, müssen Sie durch Versuche den Mittelwert bestimmen. Auf der Scheibe für den Ausdruck sind die
Drehzahlen auf den Ringen angeschrieben.
Wenn Sie die später zu bewältigende Last nicht simulieren oder beim Versuch nachbilden können,
sollten Sie je nach Motortyp mit einer Differenz von bis zu 30 % zwischen Leerlauf–
und Lastdrehzahl rechnen. Dieser Unterschied ist bei Glockenankermotoren deutlich kleiner.
Tipp: Suchen Sie im Conrad–Katalog einen vergleichbaren Motor,
bei dem beide Werte angegeben sind, und rechnen Sie die Differenz dann auf Ihre Drehzahl um.
Stirnzahnrad–Getriebe
Bei Riemen–, Schnur– und Reibrollenantrieben entspricht das Über– oder Untersetzungsverhältnis dem
(eventuell umgekehrten) Verhältnis der wirksamen Durchmesser der Scheiben: U = d2
÷ d1.
Kettenantriebe entsprechen in diesem Punkt Stirnzahnrad–Getrieben. Die Laufrichtung der verbundenen Kettenräder wird jedoch nicht invertiert.
Bei Modellbahnen kommen vorwiegend Stirnrad–, Schnecken– und kombinierte Schnecken–Stirnrad–Getriebe zum Einsatz.
Bei mehrstufigen Getrieben ist die Gesamt–Untersetzung (oder –Übersetzung) immer gleich dem Produkt
der einzelnen Stufen, also Uges =
U1 × U2 ×
U3 ….
Das Übersetzungsverhältnis entspricht bei Stirnzahnradgetrieben dem (umgekehrten) Verhältnis
der Zähnezahlen der einzelnen Räder: U =
z2 ÷ z1.
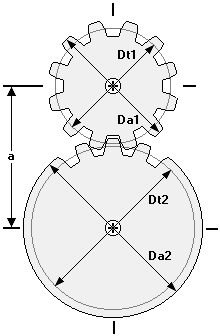
Für Stirnzahnräder sind folgende Werte wichtig: Der Außendurchmesser Da,
der Teilkreis–Durchmesser Dt, der Innen–Durchmesser Di, die Dicke h und das
Link zum Glossar
Modul m.
Das Modul ergibt sich, wenn der Teilkreis durch die Zähnezahl z geteilt wird.
Je feiner es ist, desto kleiner werden Zahnrad und Zähne bei gleicher Zähnezahl.
Nur Zahnräder und Schnecken mit gleichem Modul können kombiniert werden.
Der benötigte Achsabstand a lässt sich (ohne die übliche Luft von knapp 0,2 mm)
mit folgender Formel berechnen: (z1
+ z2)
÷ 2 × m = a (in mm).
Der Teilkreis–Durchmesser entsteht durch Multiplikation der Zähnezahl mit dem Modul:
z × m = Dt (in mm).
Der Außen–Durchmesser kann ebenfalls berechnet werden: (z + 2)
× m = Da (in mm).
Wie erwähnt, sollten etwa 0,16 bis 0,2 mm Luft
zwischen den Getrieberädern bleiben. Das lässt sich bei der Montage und Anpassung oft
durch Einlegen eines Stückchens Kupferdraht aus dünnen Litzen regeln.
Schnecken–Getriebe
Aus Platzgründen sind Schnecken–Getriebe oft die erste Wahl bei Modellbahn–Getrieben,
weil sie auf viel kleinerem Raum als Stirnzahnräder hohe Untersetzungen erreichen
und gleichzeitig noch die Drehrichtung um 90° wenden.
[ b ].
Im Gegensatz zu Stirnzahnrad–Getrieben sind Schneckengetriebe in der Regel selbsthemmend (der Antrieb
kann von der Abtriebsseite nur gedreht werden, wenn die Schneckengänge sehr schräg sind). Das und die hohe
Untersetzung bedeuten, dass Schwungmassen vor der Schnecken–Untersetzung, meist also
direkt auf der oder einer der Motorwellen, angebracht sein müssen, um ihre Trägheits–Wirkung zu behalten.
Die Untersetzung eines Schnecken–Getriebes entspricht dem Verhältnis der Zähnezahl des Schneckenrades
zur Zahl der „Gänge” der Schnecke (U = z
÷ g). Schnecken sind meist ein– oder höchstens
zweigängig. Zweigängige Schnecken haben zwei parallel zueinander laufende Spiralen um den Kern.
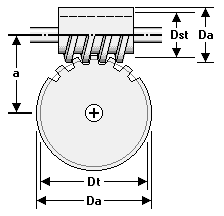
Der Teilkreis–Durchmesser der Schnecke (hier: Dst) wird bei bekanntem
Außendurchmesser wie folgt berechnet: Da - 2 × m
= Dst (in mm).
Besonders hohe Untersetzungen entstehen durch die Kombination zweier Schneckengetriebe.
Das macht zum Beispiel Sinn, wenn Bewegungen in einer geraden Linie sehr langsam ablaufen sollen.
Dazu wird ein Schneckenrad in der Bohrung mit einem Gewinde versehen, in das
eine verschieb– aber nicht verdrehbare Gewindestange eingelegt wird. Ein Motor mit
Schnecke treibt das Schneckenrad. Um die in einer bestimmten Zeit bei einer bestimmten
Schneckenrad–Drehzahl zurückgelegte Strecke der Gewindestange zu ermitteln, muss die
Steigung des Gewindes bekannt sein (zum Beispiel bei M3 0,5 mm,
M5 0,75 mm und M6
1,0 mm). Diese Technik wird oft bei motorischen Weichen– und Signalantrieben verwendet.
Getriebe–Auslegung für Fahrzeuge
Das Folgende gilt für Eisenbahn–Triebfahrzeuge ebenso wie für Modellautos.
Bedenken Sie dabei, dass Sie im Analog–Betrieb eventuell nicht die gesamte verfügbare
Spannung benutzen, sondern einen Teil davon für andere Zwecke als den Antrieb „abzwacken”
möchten. Mehr dazu findet sich bei Elektrik und Elektronik.
Sie benötigen den Treibrad–Außendurchmesser im Vorbild (D), die Motordrehzahl je Minute
unter Last (n) und die gewünschte Vorbild–Geschwindigkeit (V). Dann gilt
U = (0,188 ×
D × n) ÷ V.
Hier folgt ein kompletter Rechenweg für Modellmaße.
Der Radumfang des Modells ist Ur =
Pi × Dr.
Link zum Glossar
Pi ist etwa 3,1416.
Der in einer Minute zurück zu legende Weg s in Zentimetern
bei Vorbild–Geschwindigkeit V mit km/h ist
s = (km ×
1000 m × 100 cm)
÷ Maßstab M ÷ 60 Minuten. Das lässt sich bequem umstellen
und kürzen auf km ÷
Maßstab M × 1.666,7. Die Zahl 1.666,7 ergibt sich aus der Berechnung der Konstanten
(1.000 m × 100 cm ÷ 60 Minuten).
Nun dividieren Sie diese Strecke s durch den Radumfang des Modells in Zentimetern,
um zu erfahren, wie oft sich das Rad drehen muss, um die gewünschte Geschwindigkeit zu erreichen.
nr = s ÷
Ur.
Die Untersetzung des Getriebes beträgt nun Motordrehzahl geteilt durch Raddrehzahl:
U = n ÷
nr.
Anwendungsbeispiel
Eine Lokomotive soll eine Höchstgeschwindigkeit von 40 km/h haben. Ihre Treibräder haben am
Link zum Glossar
Laufkreis
30 mm Durchmesser. Der Maßstab sei 1:22,5
und die Motordrehzahl unter Last bei der gewünschten Spannung 8.000 U/min.
Radumfang: Ur = 30 × 3,1416
= 94,2 mm
= 9,42 cm.
Strecke: s = 40 ÷
22,5 × 1.666,7 = 2.963 cm
oder 29,63 m. Diese Strecke soll die Lokomotive in einer Minute zurücklegen.
Rad–Umdrehungszahl: nr =
2.963 cm ÷
9,42 cm = 314,5.
Getriebe–Untersetzung: U = 8.000
÷ 314,5 = 25,44.
Sie benötigen in diesem Fall also beispielsweise ein einstufiges Schnecken–Getriebe mit
einer eingängigen Schnecke und einem Schneckenrad mit 25 Zähnen oder eine zweigängige Schnecke mit einem 50–Zähne–Schneckenrad.
Schwungmassen
Heutzutage wird die Mehrheit der Modellbahn–Triebfahrzeuge digital betrieben. Besonders
in Nenngröße IIm
gibt es oft genug Platz für Puffer–Kondensatoren, idealer Weise Gold Caps.
Diese Pufferung hilft Lokomotiven ebenso wie
eine mechanische Schwungmasse, stromlose Abschnitte zu überbrücken, beispielsweise bei Weichenherzstücken
oder verschmutzten Gleisen. Beide simulieren die Massenträgheit des Vorbilds, also lange Anfahrts– und noch längere Bremswege.
Mechanische Schwungmassen sind auch im Analog–Betrieb wirksam. Es gibt aber noch einen Unterschied.
Im Gegensatz zu den Kondensatoren sorgen Schwungmassen für einen sauberen Rundlauf ohne
Schwankungen in der Stromaufnahme. Sie geben die gesammelte Energie gleichmäßig und
vielleicht noch schneller als die Kapazitätsspeicher ab, vor allem bei nur kleinen
Schwankungen der Belastung. Ihre Vorteile spielen sie besonders bei Schneckengetrieben aus, da sie einen Teil der Selbsthemmung auffangen.
Fazit: Wenn es der Platz erlaubt, sollte eine passend dimensionierte Schwungmasse vorgesehen werden. Die gar nicht so große Scheibe auf dem Bild im letzten Abschnitt sorgt unter Idealbedingungen für bis zu 60 Zentimeter Auslauf, im „Normalfall” immerhin noch für 30 Zentimeter - genug für jedes Weichenherzstück.
Wichtig: Schwungmassen müssen rund sein und dürfen keine nennenswerte Unwucht haben.