Modellbau: Grundlagen
Mathematik
„Ohne Formel kein Gemormel
”, pflegte der Mathematik–Lehrer zu sagen. Da hatte er recht!
Ob es sich nun um Umrechnung von Maßstäben, Berechnung zu Steigungen, Volumen und Gewichten oder zur Form von
Einzelteilen dreht: Ohne „Mathe” und die Kenntnis der nötigen Rechenwege und Formeln geht beim Eisenbahn–Modellbau
herzlich wenig. Die wichtigsten davon, vor allem aus dem Bereich angewandter Geometrie, werden hier aufgeführt.
Die folgenden Formeln und praktischen Anwendungs–Beispiele erheben keinen Anspruch auf Vollständigkeit,
decken aber einige wichtige oder zumindest typische Aufgaben bei Modellbau und Modellbahn ab.
Formeln zum Thema Elektrik und Elektronik finden Sie im entsprechenden Bereich,
die zu Getriebeauslegungen bei Antriebe und Getriebe.
Abschnitte dieser Seite:
- Geometrie (1): Rechteck, Quader, Dreieck
- Geometrie (2): Kreis, Kreisab– und –ausschnitt
- Geometrie (3): Zylinder
- Steigungen
- Maßstabs–Umrechnung (Verhältnisrechnung, Dreisatz)
Geometrie (1): Rechteck, Quader, Dreieck
Ein Rechteck mit den Kantenlängen a und b hat die Fläche
a × b und den Umfang 2 × (a + b).
Ein Quader mit den Kantenlängen a, b und c hat den Rauminhalt (Volumen) a × b × c.
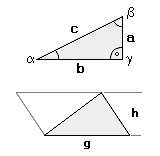
Die Fläche eines Dreiecks ist die Hälfte eines Rechtecks mit der Grundlinie g und der Höhe
h (das gilt auch für nicht rechtwinklige Dreiecke). Der Umfang eines Dreiecks ist die Summe seiner Kantenlängen. Die Summe
aller Winkel im Dreieck beträgt 180 °. Sind also zwei Winkel bekannt, kann der dritte einfach errechnet werden.
Der Satz des Pythagoras
gilt nur für rechtwinklige Dreiecke und lautet a² +
b² = c². Daraus lässt sich ableiten:
- a² = c² - b².
- b² = c² - a².
- c = Wurzel aus (a² + b²).
- a = Wurzel aus (c² - b²).
- b = Wurzel aus (c² - a²).
Die Kante „c” des rechtwinkligen Dreiecks wird „Hypotenuse” genannt.
Anwendungsbeispiel
Um die Buckelbleche eines Klappdeckelwagens aus Dreiecken zusammen setzen zu können, möchten Sie
wissen, wie lang das Maß „h” ist, also das von der Grundlinie zur Spitze des Dreiecks.
Die Buckel sollen eine Tiefe von 3 mm haben. Dazu wird ein Dreieck
halbiert, sodass es aus zwei gleichen, gespiegelten rechtwinkligen Dreiecken besteht. Angenommen sei
eines der unteren oder oberen Dreiecke mit einer Grundlinie von 81 mm.
Die Kante „a” ist die Tiefe von 3 mm. Die Kante „b” das Maß von der Grundlinie zur Spitze in der Seitenansicht
(zum Beispiel 26,5 mm), und „c” die Hypotenuse, soll ermittelt werden.
- c² = 3² + 26,5².
- c² = 9 + 702,25, also 711,25.
- c = Wurzel aus 711,25 = 26,67 mm.
Das gleichschenklige Dreieck für das Buckel–Viertel muss also eine Grundlinie von
81 mm und eine (in der Mitte angezeichnete) Höhe von 26,7 mm haben.
Geometrie (2): Kreis, Kreisab– und –ausschnitt
Bei nahezu allen Kreisbereichnungen werden Sie die Kreiszahl
Link zum Glossar
Pi benötigen.
Für Modellbauzwecke genügt eine Rundung auf 3,14159 oder 3,1416.
Ein Kreis hat den Halbmesser r und den Durchmesser d. Sein Umfang U
ist d × Pi. Seine Fläche A entspricht
r² × Pi.
Ein Kreisausschnitt hat die Form eines Tortenstücks. Seine Bogenlänge b ist
(r × Pi ×
α)
geteilt durch 180°. Die Fläche A beträgt
(b × r) ÷ 2
oder, wenn Sie b nicht kennen, (r² ×
Pi × α)
÷ 360°.
In beiden Fällen ist Pi der Mittelpunktswinkel.
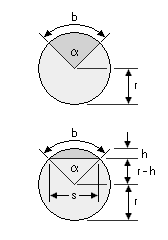
Ein Kreisabschnitt hat die Form eines Bogens mit der Sehne.
Seine Fläche wird ermittelt, indem von der des entsprechenden Kreisausschnitts die des
Dreiecks abgezogen wird, das durch den Kreismittelpunkt und die Sehne gebildet wird.
Eine Annäherung ist A =
(2 ÷ 3)
× s × h. Dazu muss die Höhe „h” allerdings bekannt sein. Bei bekannter
Länge der Sehne „s” ist diese jedoch wiederum mit Pythagoras' Hilfe zu ermitteln
(siehe nächstes Anwendungsbeispiel).
„s” lässt sich wie folgt ermitteln: s = 2 × Wurzel aus (h ×
(2 × r - h)). Wird die Formel umgestellt,
kann bei bekannter Höhe h und Länge s auch der Radius errechnet werden, zum Beispiel für ein Waggondach aus der Stirnansicht einer Zeichnung.
2 × r = (s ÷
2)² ÷ h + h.
Anwendungsbeispiel 1
Sie möchten für eine Lampe mit Blechschirm einen Kegel bauen, der einen Durchmesser 2 × r,
hier 25 mm, und eine Höhe h von 5 mm
haben soll. Der Umfang U beträgt 78,5 mm.
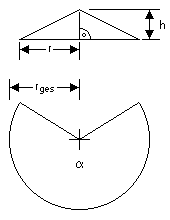
Nun berechnen Sie mit Pythagoras' Lehrsatz den Radius rges der Abwicklung,
also der Schräge in der ersten Zeichnung des Abschnitts. Er ist die Wurzel aus r² +
h², also 25,5 mm.
Sie teilen r durch rges und
erhalten 0,98. Multiplizieren Sie 360° mit diesem Ergebnis. Die Abwicklung
des Lampenschirms muss also einen Radius von 12,25 mm
und einen Winkel α von 353° haben.
Anwendungsbeispiel 2
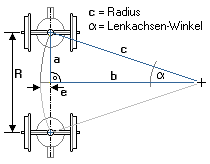
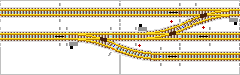
Sie möchten wissen, wie weit ein Wagen mit Drehgestellen oder ein Zweiachser bei einem bestimmten Achsstand und Gleisradius
in der Mitte ausschwenkt, um die nötige Erweiterung des Link zum Glossar
Lichtraumprofils zu berechnen. Das zweite Bild des Abschnitts zeigt die Situation.
[ b ].
Da das Maß „a” bekannt ist (halber Achsstand) und „c” auch (Radius des Gleises), kann „b” leicht berechnet werden.
Bei 133,33 mm Radstand (3,0m : 22,5) ist „a” 66,67mm und „c” (Radius) sei
930mm. Sie berechnen „b” mit dem Satz des Pythagoras und erhalten 927,61 mm.
Die Differenz zwischen „c” und „b” ist die seitliche Auslenkung (2,39 mm).
Um auch zu erfahren, in welchem Winkel die Achsen einschlagen würden, damit sie rechtwinklig zum Gleis stehen, müssen Sie die
Trigonometrie bemühen. Hier vorab die Lösung: α =
Arcussinus(a ÷ c) × 180 ÷
Pi.
Der Arcussinus ist der Winkel, dessen Sinus das Ergebnis der ersten Division
(a ÷ c) ist.
Die Lösung ist mit Absicht so formuliert, dass sie in Tabellenkalkulations–Programmen
wie Microsoft® Excel
anwendbar ist. Dort müssen Sie die Werte durch Zellenbezüge und das Symbol für Pi durch die
Funktion „PI()” ersetzen. Eine entsprechende Tabelle finden Sie bei den Downloads.
Anwendungsbeispiel 3
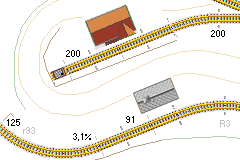
Die Länge der Mittellinie eines gebogenen Gleises mit 22,5° Mittelpunktswinkel
α und 117,5 cm Radius r
soll ermittelt werden, um die Bogenlänge b zur Berechnung von Steigungen nutzen zu können.
b = r × 2 × Pi
÷ (360 ÷
α).
Die Formel wurde auf 360°–Basis aufgebaut, weil Sie dadurch für
„360 ÷ α” einfach
die Zahl der Gleise einsetzen können, die einen Vollkreis ergeben, hier also 16:
360° ÷ 22,5°.
Die Lösung im konkreten Beispiel lautet also b
= 117,5 × 2 × 3,1416 ÷ 16 =
46,14 cm.
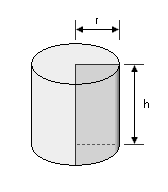
Geometrie (3): Zylinder
Wie bei vielen gleichmäßigen Körpern ist das Volumen eines Zylinders oder Zylinderaus– oder –abschnitts gleich der Grundfläche „A”
× der Höhe „h”. Die Oberfläche ist die Summe aus der Kreisfläche der beiden Stirnseiten und der Abwicklung des Mantels, also Umfang × Höhe.
Anwendungsbeispiel
Der hohle Kessel einer Modellbahn–Dampflok soll mit Blei gefüllt werden. Sie möchten wissen, wie schwer das Gewicht werden wird.
Um die Sache nicht ganz so leicht zu machen, soll unten am Gewicht eine Nut von 3 × 3mm
für die Durchführung von Kabeln bleiben. Der zylindrische Hohlraum des Kessels soll 40 mm
Durchmesser bei einer Länge von 110 mm haben.
Das spezifische Gewicht (die „Dichte”) von Blei beträgt 11,34. Blei ist also um diesen Faktor
schwerer als Wasser. Es ist zugleich der Multiplikationsfaktor, um vom Volumen auf das Gewicht zu schließen.
Zunächst muss die Fläche des vollen Kreises einer Stirnseite des Zylinders berechnet werden. Die Formel lautet
A = r² × Pi.
Das ist in diesem Fall 20² × 3,14159 und damit 400 × 3,14159,
also 1.256,64 mm² oder rund 12,6 cm².
Nun wird die Fläche der Nut benötigt, das sind a × b = 9 mm².
Dieser Wert wird von der Stirnfläche abgezogen. Es bleiben 1.247,64 mm². Das Ergebnis
wird mit der Länge des Profils multipliziert. 1.247,64 mm² × 110 mm =
137.240 mm³ oder 137,2 cm³. Das Ergebnis, multipliziert mit
der Dichte, ergibt das Gewicht des Blei–Ballasts bei idealer Ausnutzung des verfügbaren Raums: 1.559 g.
Steigungen
Steigungen und Gefälle werden in Promille, Prozent oder als Verhältnis des Höhenunterschieds „h”
zur Streckenlänge „s” ausgedrückt, wobei der Nenner so gekürzt wird,
dass der Zähler 1 beträgt. Bei der Modellbahn sind Angaben in Prozent üblich, beim Vorbild in Promille.
Die Umrechnung von Streckenlänge „s” und Höhe „h” zur Verhältniszahl: 1 ÷ v =
s ÷ h. Bei 240 cm Streckenlänge
und 96 mm Höhe ergibt sich 1 ÷
v = 240 ÷ 9,6
= 1÷25.
Die Umrechnung von Verhältniszahl zu Prozent: Steigung in Prozent = 100
÷ Nenner der Verhältniszahl, hier also
p = 100 ÷ 25 = 4 %.
Die Umrechnung von Prozent zu Verhältniszahl: Bei bekannter Höhe „h” gilt
v = h ÷ p × 100, hier also
v = 9,6 ÷ 4 × 100
= 240 cm.
Bei bekannter Streckenlänge „s” gilt h = s × p ÷ 100,
1 ÷ v = s ÷ h, hier also
h = 240 × 4 ÷
100 = 9,6 cm,
1 ÷ v =
240 ÷ 9,6 = 1÷25.
Ermittlung des Höhenunterschieds „h” bei bekannter Streckenlänge „s”:
h = s × p, also 240 × 4% = 9,6.
h = s ÷
Nenner von v, also 240 ÷ 25 = 9,6.
Ermittlung der benötigten Strecke für den Höhenunterschied „h”:
s = h ÷ p ÷ 100,
also 9,6 ÷ 0,04 = 240.
s = h × Nenner von v, also 9,6 × 25 = 240.
Beachten Sie bitte, dass diese Berechnungen die nötigen Ausrundungen am Steigungsbeginn und –ende nicht berücksichtigen.
Maßstabs–Umrechnung (Verhältnisrechnung, Dreisatz)
Die folgende Rechnung dürfte bekannt sein: Vorbildmaß ÷ Maßstab = Modellmaß, zum Beispiel
3.000 mm ÷
22,5 = 133,33 mm.
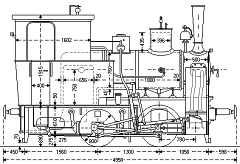
Was ist aber, wenn Sie ein Vorbildfoto oder eine Zeichnung haben und dessen oder deren
Maßstab unbekannt ist? Haben Sie ein Bezugsmaß (beispielsweise den Radstand), können
Sie andere Maße leicht ermitteln. Vorsicht: Das gilt bei Fotos natürlich nur,
wenn das Objekt rechtwinklig und nicht zu verzerrt aufgenommen ist.
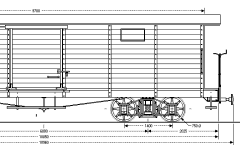
Als Beispiel sei das Foto eines Packwagens angenommen. Das Bild liegt Ihnen digital vor.
Sie wissen oder vermuten, dass der Wagen 3,60 m Radstand hat.
Von der Mitte des einen zum anderen Achslagergehäuse messen Sie im Bildbearbeitungs–Programm 186 Pixel Abstand.
Gesucht wird nun der Umrechnungsfaktor „x” von den Bildschirmpunkten (Pixeln) zu einem Maß in Millimeter für ein Modell im Maßstab
1:22,5. Da entsprechen 3,60 m Radstand 160 mm.
Faktor x = 186 ÷
160 = 1,1625.
Auf dem selben Foto messen Sie nun eine Wagenkastenlänge von 307 Pixel (Bildpunkten). Wie lang wäre der Wagenkasten im Original?
Länge l (Modell) = 307 ÷ Faktor x (1,1625)
= 264,1 mm.
264 mm × 22,5 =
5.940 mm. Dieses Maß scheint plausibel zu sein.
Wenn Sie multiplizieren statt dividieren wollen, teilen Sie im Beispiel das
kleinere durch das größere Maß, also Faktor y = 160
÷ 186 = 0,86.
Länge l (Modell) = 307 × Faktor y (0,86)
= 264 mm.
Werden diese Faktoren auf die Höhe des Wagenkastens übertragen, ergibt sich eine Höhe von etwa 1.994 mm -
das ist sogar auch plausibel. Bedenken Sie dabei, dass die Menschen zu der Zeit, als der Wagen
gebaut wurde, im Durchschnitt noch sehr viel kleiner waren als heute.